2.1. Quantum materials for energy
2.1.3. Topological insulators
Topological Insulators are materials which are bulk insulators but exhibit conducting surface states. These surface states require strong spin-orbit interaction, are highly spin polarized, have their spin locked perpendicular to the electron momentum, enjoy protection of their existence by time-reversal symmetry and have promising implications for electrical transport and spin transport. They exist as two-dimensional topological insulators with protected one-dimensional edge states and three-dimensioanal topological insulators with protected two-dimensional surface states. In both cases the dispersion near the Fermi energy is that of massless Dirac fermions, and on three-dimensional topological insulators they form a Dirac cone similar to graphene. In graphene, the Dirac cone is characterized by a pseudospin, in topological insulators by the real spin. Topological insulators are characterized mathematically by a topological invariant n which is an odd integer. Along with the topological invariant n also other quantities such as the electrical conductivity are robust, and the discrete value n=1 leads to a discreteness or quantization of the conductivity - the robustness of this quantization renders it extremely accurate. This has been demonstrated for two-dimensional topological insulators from HgTe quantum wells in 2007. The first three-dimensional topological insulators studied are Bi1-xSbx, Bi2Te3, and Bi2Se3 (Figure 3), of which the latter two have emerged as standard systems, due to their simple electronic structure with one surface state and their two-dimensional geometry which allows for simple cleavage.
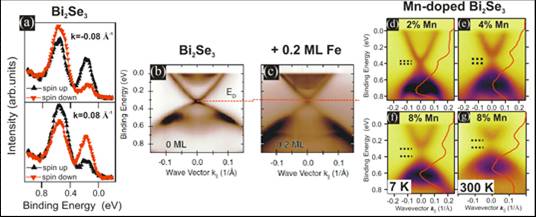
Figure 3. (a) Spin-resolved photoemission from Bi2Se3 showing ~50% spin polarization in the surface state at ~0.2 eV binding energy while the bulk admixture reduces the polarization at 0.6 eV. (b, c) The Dirac point of Bi2Se3 remains intact after deposition of 0.2 monolayer Fe at low temperature (8 K) where the surface doping becomes p-type and modifies the dispersion. (d-g) Mn doping in the bulk opens a large (~100 meV) gap in the Dirac cone but it does not change with temperature indicating that it may not be due to ferromagnetic order. (Courtesy O. Rader, HZB).
It has been shown by ARPES that the states are robust against surface impurities in line with the topological protection, that their spin polarization is high, and that they can be modified by surface doping. It has been shown at BESSY II that they are tolerant towards deposited magnetic moments. An external magnetic field or exchange field is expected to open a gap but attempts to demonstrate this with three-dimensional topological insulators have failed so far. With the inclusion of ferromagnetically ordered magnetic moments, new topological phases are predicted such as the quantized anomalous Hall insulator and a three-dimensional Weyl-fermion system.
Other important questions surround the scattering properties because scattering is reduced due to the high spin-polarization and time-reversal symmetry. Deviations from the circular shape of the Dirac cone can lift these constraints. Related to this is the electron-phonon coupling the strength of which is controversial. Topological insulators have promising optical properties in the infrared range and circularly polarized light is considered to allow for photo-induced spin currents.
The time structure of BESSY-VSR will allow for angle-resolved time-of-flight electron spectrometers such as the ArTOF to be employed. Using time resolved measurements, the evolution of the electronic structure can be probed by ARUPS/ARPES measurements, chemical changes can be monitored through time-resolved chemical shift measurements and structural changes can be studied by following the evolution of the Photoelectron Diffraction patterns.