Öffnet in neuem Fenster Opens in a new window Öffnet externe Seite Opens an external site Öffnet externe Seite in neuem Fenster Opens an external site in a new window

Gregor Schiwietz

Auger- and delta-electron emission in coincidence with scattered projectiles and charged target atoms

The measurement of triple coincidences in ion-atom collisions may involve the following:

  1. An ion beam of well defined charge state enters the magnetically shielded scattering chamber.
  2. One of the ions collides with a single target atom that effuses from a gas inlet just above the scattering center.
  3. The atom is ionized and the projectile is scattered under a certain angle.
  4. The ejected electron (green track) may be detected with an electron time-of-flight analyzer and at the same time a positive potential may be applied to the gas inlet system.
  5. The scattered projectile (dark blue track) may be measured with a position-sensitive detector to determine the projectile-scattering angle, respectively the impact parameter.
  6. Now we already have a double coincidence: ELECTRON as well as PROJECTILE from the same collision event are detected simultaneously.
  7. The pulsed positive potential at the gas inlet repels the positively charged recoil ion (light blue track) into a recoil time-of-flight analyzer, where the time information may be used to determine the charge state of the recoil ion.
  8. Now we have a triple coincidence: ELECTRON, PROJECTILE-ION as well as RECOIL-ION from the same collision event have been detected. This means, we know the impact parameter (or equivalently the projectile scattering angle), the target mass and charge state, as well as the momentum vector of the ejected electron.

 

Selected references on ion-atom coincidence experiments:

  • "High Ionization Probabilities in 30-, 100-, and 300-keV Proton-Helium-Collisions" G.Schiwietz, Phys.Rev. A37, 370-376 (1988)
  • "Investigation of Simultaneous Inner- and Outer-Shell Ionization and Auger-Electron Emission in slow Ar+ + Ar Collisions at Intermediate Impact Parameters" G.Schiwietz, B.Skogvall, J.Tanis, and D.Schneider; Phys.Rev. A38, 5552 (1988)
  • "Ionization and Autoionization in Small Impact Parameter p + He and in High Energy Ne10+ + He Collisions" G.Schiwietz, B.Skogvall, N.Stolterfoht, D.Schneider, V.Montemayor ,and H.Platten, Nucl.Instr.Meth. B40/41, 178-183 (1989)
  • "Evidence for Electron Correlation in the Two-Electron Continuum During Double Ionization in 300-keV p + He Collisions" B. Skogvall and G. Schiwietz, Phys.Rev.Lett. 65, 3265 (1990)
  • "Double Ionization of Helium by 40 MeV Protons" G. Schiwietz, G. Xiao, P.L. Grande, B. Skogvall, R. Köhrbrück, B. Sulik, K. Sommer, A. Schmoldt, U. Stettner, and A. Salin, Europhys.Lett. 27, 341-346 (1994)

The following animation displays a scatter plot of the double-coincidence events (time-of-flight of an ejected electron and a recoil ion) for 40 MeV Proton + Helium collisions. Each dot on the screen corresponds to a single coincidence event. The electron time-of-flight is measured with respect to the pulsed ion beam (cyclotron frequency) and the recoil-ion time-of-flight is measured with respect to the pulsed electrostatic field mentioned above. The animation covers a time slice of about 2 hours out of a few days continuous experimental time (beam time). The strong horizontal line in the lower part of the plot corresponds to coincidences between electrons and singly charged He ions. The weak horizontal line that lies somewhat lower in the plot corresponds to coincidences between electrons and doubly charged He ions. The strong line in the upper part of the plot corresponds to random coincidences with singly ionized He ions (about 20% of the true coincidences) from the subsequent beam pulse of the cyclotron.

 

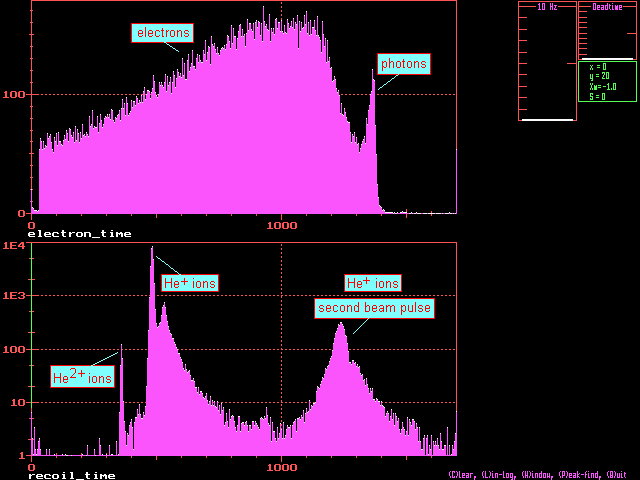
The following plot displays the spectra obtained from the projection of the above coincidence-data points on the recoil time-of-flight and the electron time-of-flight axis. One may easily distinguish between the spectrum of continuous electrons (the so-called secondary electrons or delta electrons) and a peak due to photons. Note that the recoil time-of-flight spectrum is shown with a logarithmic y-axis. As explained in reference (e) the double-ionization spectra for He ionized by fast protons (30% speed of light) show clear indications of initial-state correlation. This means, both He electrons talk to each other prior to the collision and the correlated two-electron motion determines the double-ionization probability. It is emphasized that double ionization of fast electrons would be suppressed by about an order of magnitude without initial-state correlation.

Auger- und Delta-Elektronenemission - enlarged view